3826 - 계산왕 연산군

Time Limit: 3s Memory Limit: 128MB

Submissions: 13 Solved: 2

Description

◎ : {0,1,..,9} x {0,1,...,9} → {0,1,...,9} 인 연산자 ◎가 있다. 이 연산자는 0◎0 = 0 을 만족한다고 한다.

또다른 연산자 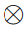$\otimes$ : Z₀ + x Z₀ + → Z₀ + 는 연산자 ◎ 을 이용해서 정의가 가능한데, p 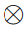$\otimes$ q 는 각 자리수마다 (p의 i번째 자리 수) ◎ (q의 i번째 자리 수) 의 결과값을 i번째 자리 수로 사용한 숫자가 결과값이 된다.

예를 들어 p◎q = (p*q)%10 으로 정의되었다면 5566 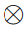$\otimes$ 239 의 결과값을 구하는 과정은 아래와 같다.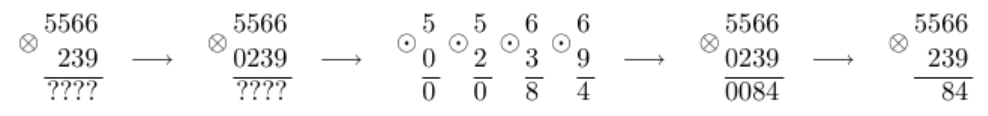

$\epsfbox{p4984.eps}$

연산자 ◎의 내용과 두 음이아닌 정수 a b가 주어졌을 때 (a≤b)

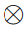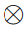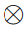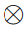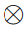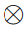a $\otimes$ (a+1) $\otimes$ (a+2) $\otimes$ ... $\otimes$ (b-1) $\otimes$ b 를 구하여라.

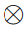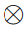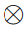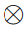$\otimes$ 연산자의 계산 순서는 왼쪽부터 계산한다. 즉, p $\otimes$ q $\otimes$ r = (p $\otimes$ q) $\otimes$ r 로 취급한다.

Input

첫 10줄 각각에는 10개의 수가 주어진다. i번째 줄의 j번재 숫자는 (i-1)◎(j-1) 의 결과값을 나타낸다. 0◎0 은 항상 0이다.

이어 11번째 줄에는 2개의 정수 a b가 주어진다. (0 ≤ a ≤ b ≤ 10^18)

Output

a부터 b까지 모든 수를 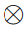$\otimes$ 연산한 결과값을 출력한다. 불필요한 0은 출력하지 않는다.

Sample Input

0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 0
2 3 4 5 6 7 8 9 0 1
3 4 5 6 7 8 9 0 1 2
4 5 6 7 8 9 0 1 2 3
5 6 7 8 9 0 1 2 3 4
6 7 8 9 0 1 2 3 4 5
7 8 9 0 1 2 3 4 5 6
8 9 0 1 2 3 4 5 6 7
9 0 1 2 3 4 5 6 7 8
0 10

Sample Output

Source

Regionals 2010, Europe - Northeastern