3139 - 우선순위 하노이 탑

Time Limit: 3s Memory Limit: 128MB

Submissions: 12 Solved: 6

Description

하노이 탑 문제는 매우 유명하다. n개의 원반이 아래의 그림처럼 크기순서대로 놓여져있을 때,

1. 크기가 작은 원판 위에 크기가 큰 원판을 놓을 수 없으며

2. 원판을 움직이는 것은, 각 기둥에서 가장 위에 있는 원판 하나만 옮길 수 있다

는 조건이 있을 때, 최소 몇변의 움직임만에 A 기둥에 있는 원판을 모두 다른 기둥으로 옮길 수 있는지 묻는 문제이다.

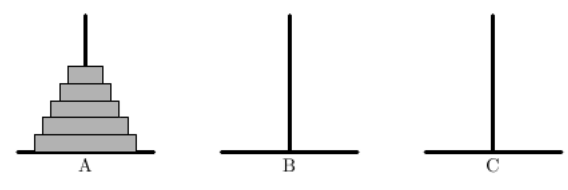
$\epsfbox{p4050.eps}$

지금 우리가 풀려는 문제도 위의 조건을 만족하면서 원판을 옮기려는건데, 새로운 정보를 이용해서 문제를 좀 더 재밌게 하려고한다. 바로 원판을 옮기는데 우선순위를 정하는 것이다.

원판을 옮기는 동작은 6가지 경우가 존재한다. AB, AC, BA, BC, CA, CB. AB가 의미하는 것은, A 기둥의 가장 위에 있는 원판을 B 기둥으로 옮긴다는 뜻이다. 나머지 5개의 동작도 마찬가지 뜻이다.

여기서 우리는 저 6개의 동작에 우선순위를 두어서, 우선순위가 높은 동작부터 수행하려고 한다. 예를 들어 우선순위가 AC AB BA BC CA CB 이렇게 지정되있으면, 가능한 이동 동작들 중에, 뒤에 있는 동작보다 앞에 있는 동작을 먼저 수행한다. 위의 그림의 상황같은 경우 A기둥에 있는 원판을 B로도 옮길 수 있고, C로도 옮길 수 있을텐데, AC가 AB보다 우선순위가 높으므로 원판을 C 기둥으로 옮겨야 한다.

우선순위만 이렇게 정의해놓으면 문제가 발생할 수 있는데, AB BA 이렇게가 가장 우선순위가 높다면 가장 작은 원판이 B기둥 A기둥을 왔다갔다만 할 것이다. 이런 문제를 막기 위해 우리는 하나의 원판이 연속으로 2번 이상 움직이는 경우도 막으려고 한다. 이 조건까지 추가하게 되면, 유한번의 이동으로 언제나 A 기둥의 모든 원판이 B 기둥, 또는 C 기둥으로 모두 옮겨지는 것이 가능하다고 한다.

원판의 개수 n과, 이동의 우선순위들이 주어졌을 때, 몇번의 움직임만에 A 기둥에 있는 모든 원판들이 B 기둥으로 옮겨지거나(이 경우 A와 C 기둥은 비어있다.) C 기둥으로 옮기지는지(이 경우 A와 B 기둥은 비어있다.) 구하시오.

Input

입력은 2개의 줄로 주어진다. 첫째줄에는 원판의 개수 n (1 ≤ n ≤ 30) 이 주어진다. 그 다음 줄에는 6개의 단어가 들어온다. 각 단어는 AB,AC,BA,BC,CA,CB 중 하나이며, 단어 사이는 띄어쓰기로 구분된다. 이는 먼저 나온 동작이 뒤에 있는 동작보다 우선순위가 높다는 뜻이다.

Output

A기둥에 있는 모든 원판을 B나 C 기둥으로 모두 옮기는데 사용된 이동횟수를 출력한다. 답은 10^18보다 크지 않다.

Sample Input

3 
AB BC CA BA CB AC 

2 
AB BA CA BC CB AC

30
BA CA AC AB CB BC

Sample Output

7 

5

137260754729765

Hint

1. 테스트를 위해서 예제를 3개 제시했으니, 실제로 채점시에는 3개의 데이터가 따로 존재한다.

2. 채점용 데이터가 100개정되 되서 미리 말해둔다. 2번째 줄의 문장의 가장 끝에는 EOF가 아니라 '\n'이 들어가있다. (그냥 getchar()로 안풀면 된다.)

Source

Regionals 2007, Europe - Northeastern