2742 - 픽셀섞기

Time Limit: 3s Memory Limit: 128MB

Submissions: 14 Solved: 7

Description

이미지의 픽셀을 섞은 행위는 원본이미지를 개판으로 뜯어고쳐버려 랜덤한 느낌의 이미지 결과물을 만든다. 하지만 이 섞는 행위를 똑같이 반복하다보면 언젠간 원본 이미지로 돌아올 것이다! 이는 딱히 놀라운 사실이 아닌데, 픽셀을 섞는 행위를 픽셀에 대한 일대일 대응함수(또는 permutation)으로 생각한다면, 유한번 반복해서 초기상태로 돌아온다는 것이 자명하기 때문이다.

이제 nxn 짜리 이미지에 대해서 "변환 연산"인 연산 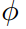$\phi$ 이 정의됐을 때, 최소 몇번의 연산 끝에 원본이미지로 돌아오는지 계산해보자. (물론 0번 보다는 많이)

예를 들어 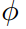$\phi$ 가 반시계방향으로 90도 돌리는 변환 연산이라면, 4번의 연산 후에는 원본 이미지로 돌아올 것이다.

$\epsfbox{p3510b.eps}$

Input

입력으로 2개의 줄이 주어진다. 첫번째 줄에는 이미지의 가로세로 크기를 나타내는 짝수 n이 주어진다. (2 ≤ n ≤ 1,024)

그 다음 줄에는 변환 연산을 나타내는 문자열이 주어진다. (최대 32개의 연산)

연산을 나타내는 문자열에는 id, rot, sym, bhsym, bvsym, div 그리고 mix 가 있으며, 문자열 뒤에 '-'가 붙어있을 수 있다. 이 경우 변환 연산의 역원을 구하는 연산으로 바뀐다. 예 들어 반시계방향으로 90도 돌리는 연산인 rot에 -가 붙은 rot- 연산의 경우는 시계방향으로 90도가 돌아간 이미지로 변환시킨다.

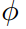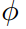입력으로 들어온 각각의 연산을 k₁, k₂,..., k_p로 표현한다면, 최종적으로 입력으로 주어진 연산 $\phi$ 은 $\phi$ = k₁ok₂o^...ok_p으로 표현된다. 즉, 이 말은 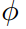$\phi$ 연산은 원본이미지에서 마지막으로 들어온 k_p연산을 거친 이미지를 입력으로 k_p-1연산을 수행하고, 이를 반복해 k₁연산까지 수행한 결과물을 출력하는 것이다.

예를 들어 입력으로 "bvsym rot-" 으로 들어온다면 왼쪽 이미지가 오른쪽처럼 변할 것이다.

$\textstyle \parbox{.25\textwidth}{ \begin{center} \mbox{} \epsfbox{p3510d.eps} \end{center}}$

각 연산에 대한 정보는 아래에 기술되있다.

$\textstyle \parbox{.70\textwidth}{ \begin{description} \vspace{.25in} \item[\te... ... , a^{n/2+1}_{2k+1} , \cdots, a^{n-1}_{2k}, a^{n-1}_{2k+1}$. \end{description}}$

영어이기도하고 기호도 추상적이지만..알아서 이해해보자. 고대 올 정도의 영어+수리 실력이면 충분히 이해하리라 믿는....

Output

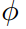$\phi$ 연산을 m번 수행했을 때, 즉 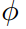$\phi$ ^m연산을 수행했을 때 결과가 원본이미지와 동일하게 되는 가장 작은 수 m (m>0)을 출력한다. m < 2³¹ 을 만족한다고 가정해도 좋다.

Sample Input

256
rot- div rot div

256
bvsym div mix

Sample Output

8

63457

Hint

문제의 이해와 프로그램 테스트를 돕기위해 sample input과 sample output을 2개 넣었지만, 실제 채점시에는 두개의 데이터가 따로 존재한다.